Operations to preserve convexity----restricted to a line

Restricting a convex function to a line geometrically means that the convex function takes values at points on the intersection of a certain line (the line being: $x + tv$) and the domain. For a convex function $f(x)$, for a point $x$ in its domain, i.e., $x \in \textbf{dom } f$, and another point $v$ such that $x + tv \in \textbf{dom } f$, the function

\[g(t) = f(x + tv)\]

is a convex function with respect to $t$.

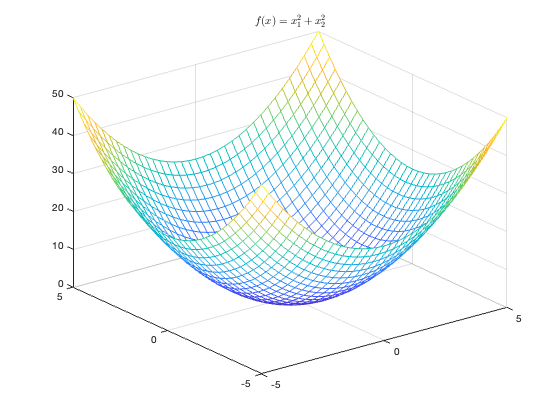
For example, $f(x, y) = x^2 + y^2$ is a convex function, and its graph is:

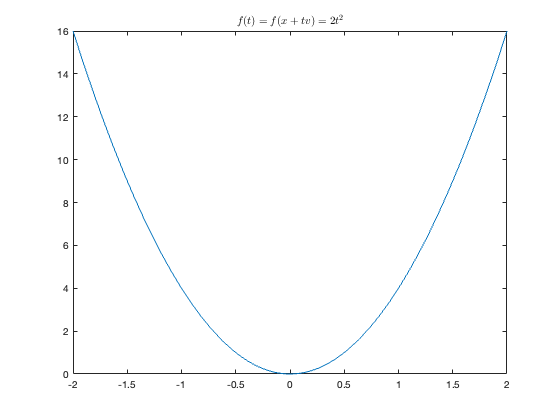
If $x = (0, 0)$, $v = (1, 2)$, then $f(x + tv) = 2t^2$, and its graph is:

Some documents suggest that restricting to a line is equivalent to the vertical cross-section of the function intersecting the function’s graph, as shown below:

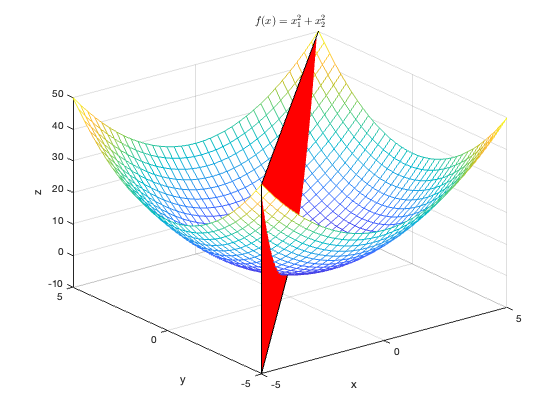
However, this is not entirely accurate, as the shape of this line depends on the values of $x$ and $v$. This is especially evident in one-dimensional functions, but they are always convex.

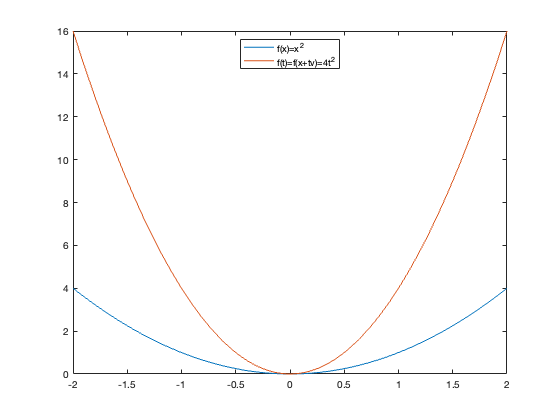
For instance, if $f(x) = x^2$, taking $x = 0$ and $v = 2$, then $g(t) = 4t^2$, and its graph is:

There is a theorem:

$f(x)$ is a convex function if and only if for any $x \in \textbf{dom } f$, $x + tv \in \textbf{dom } f$, $g(t) = f(x + tv)$ is a convex function.

Proof: Assuming $g(t)$ is a convex function, for $0 \leq \alpha \leq 1$, we have

\[\begin{aligned} \Leftrightarrow &~~ \alpha g(t_1) + (1-\alpha)g(t_2) \leq g(\alpha t_1 + (1-\alpha)t_2) \\ \Leftrightarrow &~~ \alpha f(x + t_1v) + (1-\alpha)f(x + t_2v) \leq f(x + (\alpha t_1 + (1-\alpha)t_2)v) \end{aligned}\]

Let $x = x_1, t_1 = 0, t_2 = 1, v = x_2 - x_1$,

\[\begin{aligned} \Leftrightarrow &~~ \alpha f(x_1) + (1-\alpha)f(x_2) \leq f(\alpha x_1 + (1-\alpha)x_2) \\ \Leftrightarrow &~~ f(x) \text{ is a convex function} \end{aligned}\]

$\square$