Draw animated hear by Python

Method One：
Method Two:

Stumbled upon a dynamic heart-shaped graph implemented by someone using MATLAB on a Chinese TikTok video, I got inspired to recreate it using Python. So I explored two different implementation approaches, and the result is as follows:

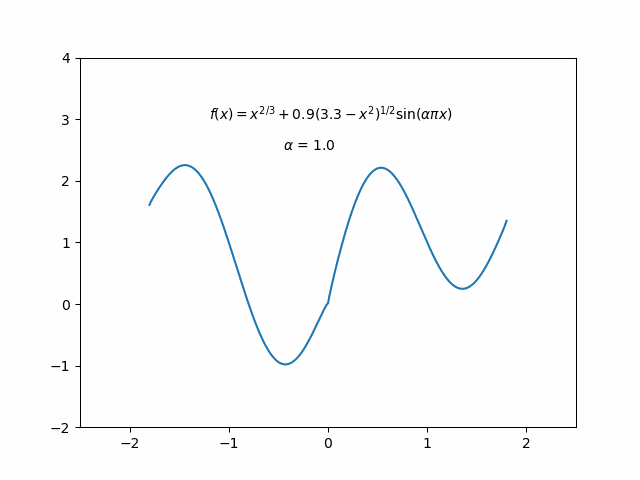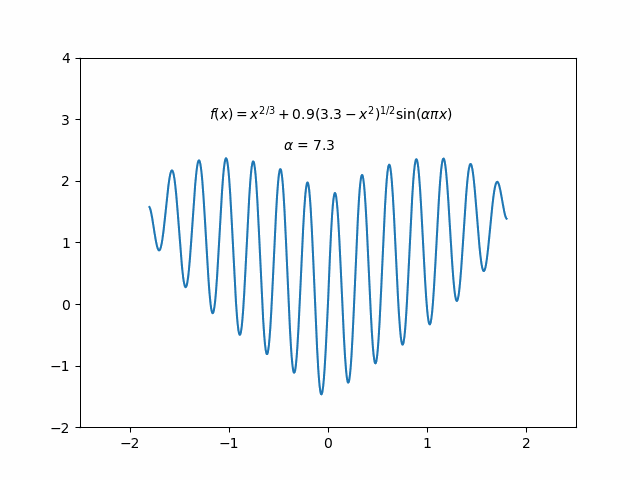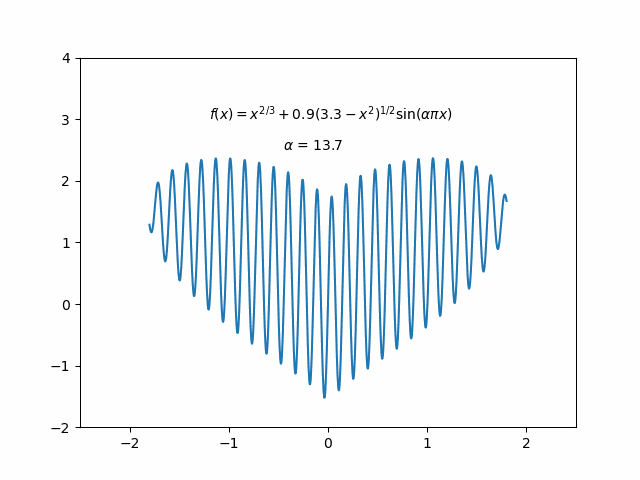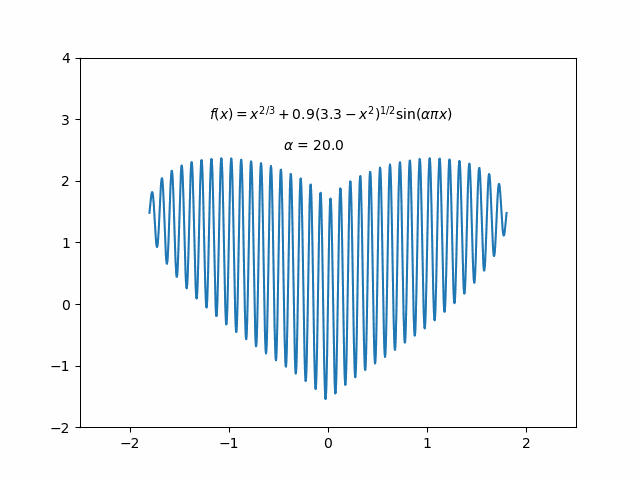
Method One：

Apply looping and combine the parameter pause, clf in pyplot to achieve dynamic image refreshing

import matplotlib.pyplot as plt
import numpy as np


# type %matplotlib qt to shown figure in a separate window
x = np.linspace(-1.8, 1.8, 1000)
alpha = 1

while alpha <= 21:
    plt.xlim(-3, 3)
    plt.ylim(-2, 4)
    y = abs(x)**(2/3) + 0.9*np.sqrt(3.3 - x**2)*np.sin(alpha*(np.pi)*x)
    plt.plot(x, y)

    plt.text(-1.6, 3, r'$f(x)=x^{2/3}+0.9(3.3-x^2)^{1/2}\sin(\alpha\pi x)$')
    alpha_s = str(round(alpha, 2))
    tx = plt.text(-0.5, 2.5, r'$\alpha=$' + alpha_s)
    plt.pause(0.02) # pause 0.02 s
    if alpha <= 20:
        alpha += 0.1
        plt.clf() # clear the current picture
    else:
        break

Method Two:

make use of the animation function in matplotlib library, achieving animation by updating the coordinates of pictures
animation can generate gif format animated picture

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation


def animate(alpha):
    x = np.linspace(-1.8,1.8,1000)
    y = abs(x)**(2/3) + 0.9*np.sqrt(3.3 - x**2)*np.sin(alpha*(np.pi)*x)
    PLOT.set_data(x, y)
    time_text.set_text(r'$\alpha$ = ' + str(round(alpha, 2)))
    return PLOT, time_text

fig = plt.figure()
ax = fig.add_subplot(111, xlim=(-2.5, 2.5), ylim=(-2, 4)) # or plt.subplot
PLOT, = ax.plot([], []) # return all the lines
plt.text(-1.2, 3, r'$f(x)=x^{2/3}+0.9(3.3-x^2)^{1/2}\sin(\alpha\pi x)$')
time_text = ax.text(-0.45, 2.5,'') # transform = ax.transAxes

ani = FuncAnimation(fig, animate, frames = np.arange(1, 20.1, 0.1), interval = 20, repeat = False)
ani.save("heart.gif") # save as one gif document

Method One：

Method Two:

Enjoy Reading This Article?