Saddle point in optimization theory

When studying the optimization course, I often hear the term “saddle point.” My teacher quickly mentioned this term but did not provide a detailed explanation of the meaning of a saddle point.

The mathematical meaning of a saddle point is: the gradient (first derivative) of the objective function at this point is zero, but in one direction from this point, it is a local maximum, while in another direction, it is a local minimum.

A sufficient condition for identifying a saddle point is that the Hessian matrix at the point where the first derivative is zero is indefinite.

• Positive semi-definite matrix: All eigenvalues are non-negative, or all principal minors are non-negative.

• Negative semi-definite matrix: All eigenvalues are non-positive, or all principal minors alternate in sign.

• Indefinite matrix: Eigenvalues have both positive and negative values, or principal minors do not satisfy the conditions of the above two cases.

A typical example of a saddle point is the point (0,0) in the function \(f(x)=x^3\), and the saddle point (0,0,0) in the function \(z=x^2-y^2\) with the Hessian matrix:

The following pictures graphically representing the saddle points of the two functions (include red points representing the saddle points):

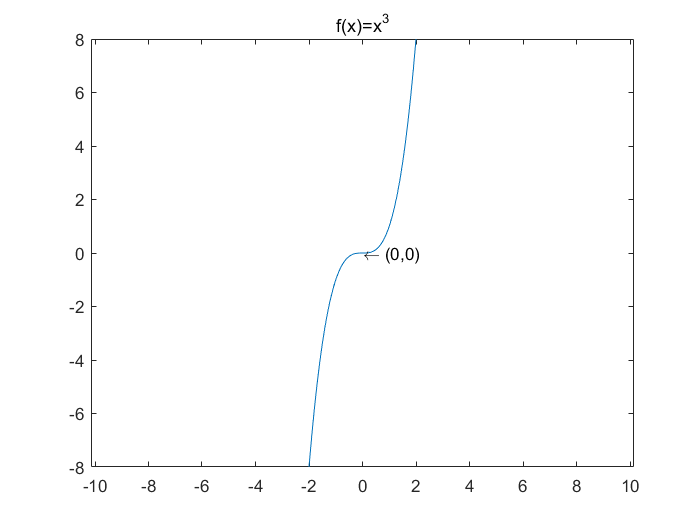
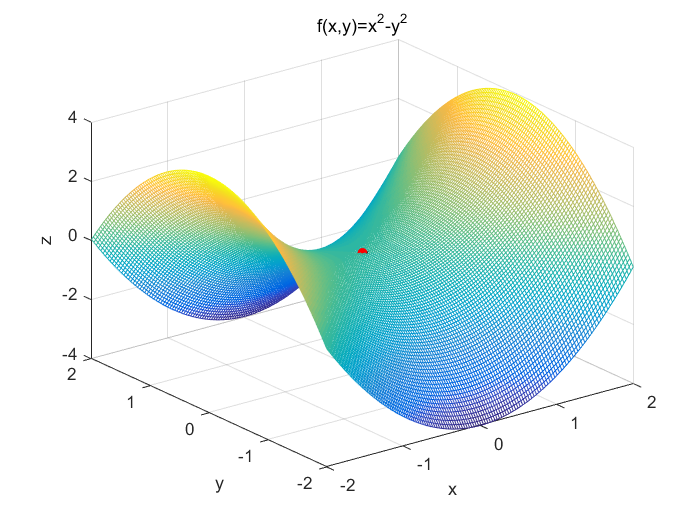
function SaddlePoint

% f(x)=x^3
x=-2:0.1:2;
y=x.^3;
plot(x,y);
axis equal;
text(0,0,'\leftarrow (0,0)');
title('f(x)=x^3');

% f(x)=x^2-y^2
figure (2);
[x,y]=meshgrid(-2:0.03:2);
z=x.^2-y.^2;
mesh(x,y,z);
hold on;
scatter3(0,0,0,'filled','MarkerFaceColor','r');
text(0,0,0,'\leftarrow');
xlabel('x');
ylabel('y');
zlabel('z');
title('f(x,y)=x^2-y^2');
hold off;
end