Lipschitz continuous and absolute continuous

• 1. Lipschitz Continuity
• 2. Absolute Continuity

1. Lipschitz Continuity

The term “Lipschitz continuity” is frequently encountered. Lipschitz continuity is stronger than ordinary continuity; it not only requires the function to be continuous but also demands that the function’s gradient is less than a positive real number.

The definition for single-variable real functions can be:

For any two points $x_1$ and $x_2$ in the domain, there exists a $K > 0$ such that

\[|f(x_1)-f(x_2)|\leq K|(x_1-x_2)|\]

For multivariable functions, it requires that the gradient with respect to any variable is less than or equal to $K$.

2. Absolute Continuity

Besides Lipschitz continuity, there is also absolute continuity, which not only requires uniform continuity but also that the function is Lebesgue integrable. The inclusion relationship among these different types of continuity on a set is:

\[\text{Lipschitz continuous}\subset\text{absolute continuous}\subset\text{uniform continuous}\subset\text{ordinary continuous}\]

The definition of absolute continuity is:

For any real number $\epsilon > 0$ and any sequence of disjoint subintervals $(x_k, y_k)$ in the domain, there exists a real number $\delta > 0$ such that when $\sum_k |x_k - y_k| < \delta$, we have $\sum_k |f(x_k) - f(y_k)| < \epsilon$. An example of a function that is uniformly continuous but not absolutely continuous is $x / \sin(1/x)$. Its graph is:

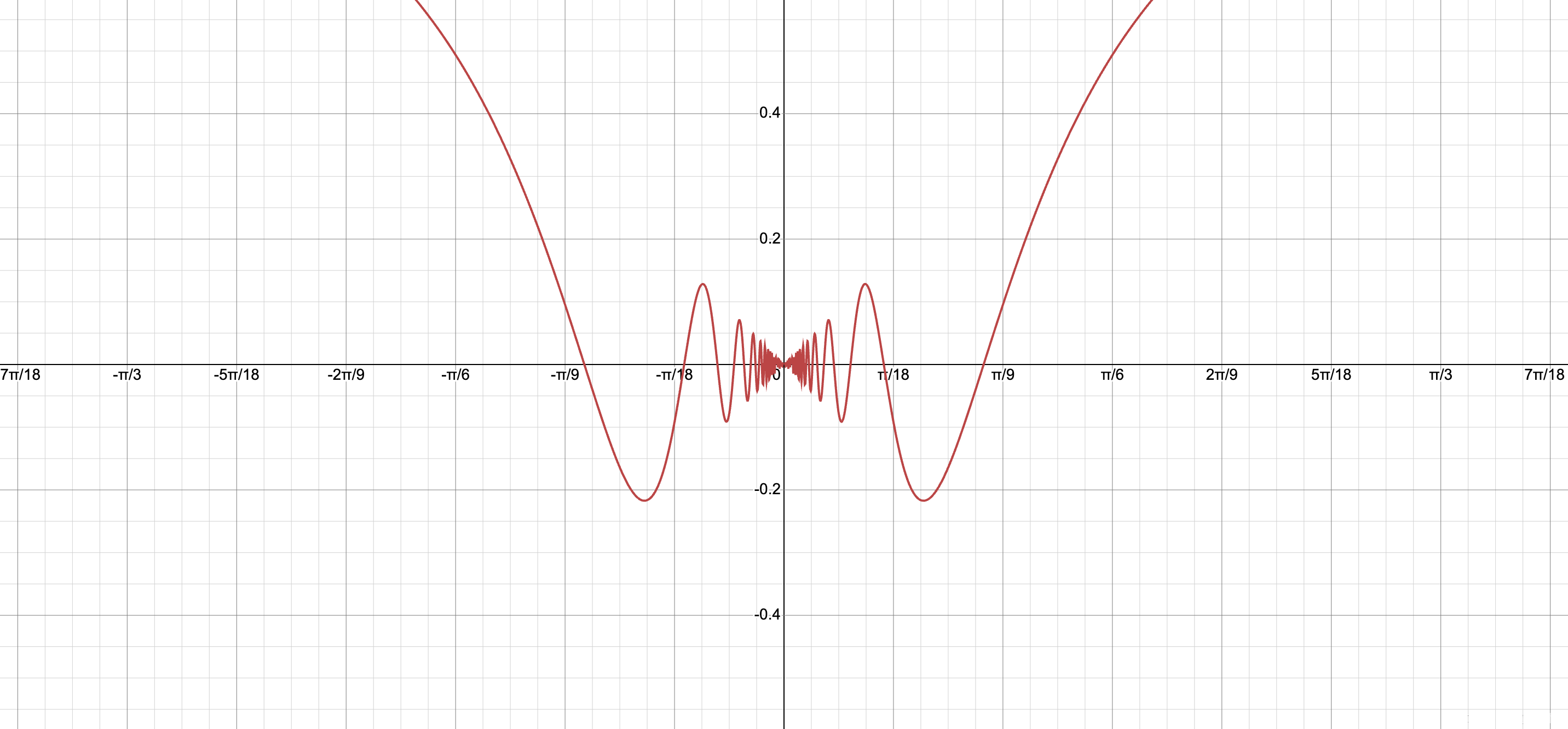
For this function, one can find disjoint subintervals in the domain whose total length is less than a constant, but the total absolute deviation in all these subintervals can reach infinity (let $x_n = \frac{1}{2n\pi + \pi/2}$, $y_n = \frac{1}{2n\pi}$, $n \geq 1$).

This function is also not Lebesgue integrable because:

\[\int_{-\infty}^{\infty}\left|\frac{x}{\sin(1/x)}\right|=\infty\]

(The integral of the absolute value of the function being not infinite is a condition for the existence of the Lebesgue integral.)