Chapter 2#
Exercise 2.1#
For each one of the following sets, determine whether it is a polyhedron.
(a) The set of all \((x, y)\in \mathcal{R}^2\) satisfying the constraints:
(b) The set of all \(x\in\mathcal{R}\) satisfying the constraint \(x^2 - 8x + 15 \leq 0\).
(c) The empty set.
Solution:
(a) The set equals \(\{ (x,y) | x \geq 0, y \geq 0, x^2 + y^2 \leq 1 \}\), which has the following image:
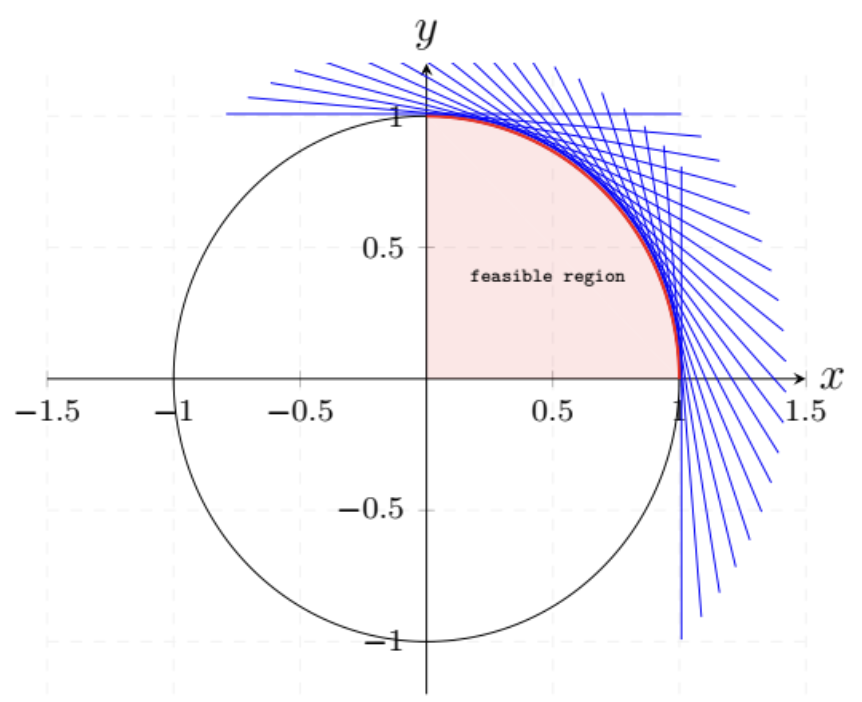
It is a set represented by infinite linear constraints, while a polyhedron is formed by finite linear constraints.
(b) The set is \(\{x\geq 3, x\leq 5\}\) and is a polyhedron.
(c) The empty set can be represented as \(\{x\geq 0, x< 0\}\) and is a polyhedron.
Note
A polyhedron is formed by finite linear constraints.
Exercise 2.2#
Let \(f:\mathcal{R}^n\rightarrow\mathcal{R}\) be a convex function and let \(c\) be some constant. Show that the set \(S = \{\bf{x} \in \mathcal{R}^n\mid f(\bf{x}) \leq c\}\) is convex.
Solution:
Assume two random element \(x_1\) and \(x_2\) in the set \(S\), therefore
For a parameter \(\theta\in [0, 1]\),
Thus,
Since \(f\) is a convex function,
And this leads to
Therefore, the set \(S\) is convex. \(\Box\)
Exercise 2.3#
(Basic feasible solutions in standard form polyhedra with upper bounds) Consider a polyhedron defined by the constraints \(\bf Ax = b\) and \(\bf 0\leq x\leq u\), and assume that the matrix \(\bf A\) has linearly independent rows. Provide a procedure analogous to the one in Section 2.3 for constructing basic solutions, and prove an analog of Theorem 2.4.
Solution:
The only difference of the above statement with Theorem 2.4 is that there are upper bounds for \(\bf x\). An analogous theorem is below:
Theorem
For a polyhedron defined by the constraints \(\bf Ax = b\), \(\bf A\) has dimensions \(m\times n\), \(\bf 0\leq x\leq u\) and \(m\) independent rows. \(\bf x\) is a baisic solutions if and only if there exists indices \(B(1), B(2),\dots, B(m)\) such that:
(a) the columns \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(m)}\) are linear independent.
(b) if \(i\neq B(1),\dots, B(m)\), \(x_i=0\) or \(x_i=u_i\).
Proof.
Assume a solution \(x\) satsifying (a) and (b), and \(U\) is the set of indecies that \(x_i=u_i\), then
Because the columns \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(m)}\) are linear independent and \(x\) is a feasible solution, the above equations have a unique solution. And thus \(\bf Ax=b\) has a unique solution. From Theorem 2.2, the \(n\) active constraints are independent and thus \(\bf x\) is a basic solution.
For the converse, we assume that \(\bf x\) is a basic solution and we will show that conditions (a) and (b) are true. Since \(x\) is a basice solution, it is the solution of \(n\) linear independent constraints. Therefore, the \(n\) columns of \(\bf A\) and all the components in \(\bf x\) form the equations:
According to Theorem 2.2, the above equations has \(n\) linear independent column vectors and thus has a unique solution. Assume \(\bf x\) has \(k\) components that \(x_i\neq 0, x_i\neq u_i\). Equivalently, \(\sum_{i=1}^k x_i\mathbf{A}_{B(i)}=b-\sum_{i\in U}x_iA_{B(i)}\) has unique solution and therefore its columns \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(k)}\) are linear independent.
We have shown that there are \(k\) independent columns in \(\bf A\) and this implies \(k\leq m\). Since \(\bf A\) has \(m\) independent rows, it also has \(m\) independent columns. Now (a) is proved and we prove (b) next. If \(i\neq B(1), \dots, B(m)\), \(i\neq B(1), \dots B(k)\) and \(x_i=0\) or \(x_i=u_i\), (b) is also satisfied.
\(\Box\)
Note
Theorem: if equations \(Ax=b\) are consistent (has feasible solution), the columns of \(\bf A\) are linearly independent if and only if \(\bf Ax = b\) has a unique solution. (similar to Theorem 1.2)
For \(n\) decision variables, \(n\) independent row constraints results in a unique solution and also results in \(n\) independent column vectors
Exercise 2.4#
We know that every linear programming problem can be converted to an equivalent problem in standard form. We also know that nonempty polyhedra in standard form have at least one extreme point. We are then tempted to conclude that every nonempty polyhedron has at least one extreme point. Explain what is wrong with this argument.
Solution:
Assume a nonempty polydron is a hyperplane \({\bf a'x}=b\), for any point \(x_0\) in it, we can find other two points \(x_1\), \(x_2\) that satisfies \(x_0 = \lambda x_1+(1-\lambda)x_2\), so there can not be an extreme point in this polyhedron.
Note
A hyperplane is a polyhedron, but it does not has extreme points.
Exercise 2.5#
(ExtreIne points of isoInorphic polyhedra) A mapping \(f\) is called affine if it is of the form \(f(\bf x) = Ax + b\), where \(\bf A\) is a matrix and \(\bf b\) is a vector. Let \(P\) and \(Q\) be polyhedra in \(\mathcal{R}^n\) and \(\mathcal{R}^m\) , respectively. We say that \(P\) and \(Q\) are isomorphic if there exist affine mappings \(f: P\rightarrow Q\) and \(g: Q\rightarrow P\) such that \(g(f(\bf x) = x\) for all \(\mathbf{x} \in P\), and \(f(g(\bf y)) = y\) for all \(\mathbf{y} \in Q.\) (Intuitively, isomorphic polyhedra have the same shape.)
(a) If \(P\) and \(Q\) are isomorphic, show that there exists a one-to-one correspondence between their extreme points. In particular, if \(f\) and \(g\) are as above, show that \(\bf x\) is an extreme point of \(P\) if and only if \(f(\bf x)\) is an extreme point of \(Q\).
(b) (Introducing slack variables leads to an isoInorphic polyhedron) Let \(P = \{\mathbf{x} \in \mathcal{R}^n \mid \bf Ax \geq b, x\geq 0\}\), where \(\bf A\) is a matrix of dimensions \(k\times n\). Let \(Q = \{\bf (x, z) \in \mathcal{R}^{n+k} \mid Ax - z = b, x \geq 0, z \geq 0\}\). Show that \(P\) and \(Q\) are isomorphic.
Solution:
(a) We first prove:if \(\bf x\) is the extreme point of \(P\), then it is also the extreme point of \(Q\).
According to the definition of extreme point and Theorem 2.3 in the book, \(\bf x\) is also a vertex of \(P\), then: there exists a vector \(\bf c\) such that \(\bf c'x<c'y\) for all \(\bf y\) satisfying \(\bf y\in P\) and \(\bf y\neq x\).
Since \(g(f(\bf x))=\bf x\),
Since \(g\) is an affine function, we assume \(g(\bf x)=Dx+d\), then
\(\bf Ax+b\), \(\bf Ay+b\) are the points in \(Q\). \(\bf c'D\) is a vector and \(\bf Ax+b \neq Ay+b\). By the definition of vertex, \(\bf Ax+b\) is the vertex of \(Q\). Thus it is also an extreme point of \(Q\).
In a similar way, we can prove: if \(\bf x\) is the extreme point of \(Q\), then it is also the extreme point of \(P\)。\(\Box\)
(b) By obtaining the formulas of \(f\) and \(g\), we can prove \(P\) and \(Q\) are isomorphic.
The formulas of \(f\) and \(g\) are below:
Exercise 2.6#
(Carath\(\acute{\bf e}\)odory’s theorem) Let \(\bf A_1,\dots,A_n\) be a collection of vectors in \(\mathcal{R}^m\).
(a) Let
Show that any element of \(C\) can be expressed in the form \(\sum_{i=1}^n \lambda_i\mathbf{A}_i\), with \(\lambda_i\geq 0\), and with at most \(m\) of the coefficients \(\lambda_i\) being nonzero. Hint: Consider the polyhedron
(b) Let \(P\) be the convex hull of the vectors \(\mathbf{A}_i\):
Show that any element \(P\) can be expressed in the form \(\sum_{i=1}^n \lambda_i\mathbf{A}_i\), where \(\sum_{i=1}^n \lambda_i=1\) and \(\lambda_i\geq 0\) for all \(i\), with at most \(m+1\) of the coefficients \(\lambda_i\) being 0.
Solution:
(a)Let \( y \) be a point in \( C \). The polyhedron
is a standard form polyhedron and is non-empty (because \(y\) is a point in it). According to Corollary 2.2 in the textbook, a non-empty standard form polyhedron must have a basic feasible solution. According to Theorem 2.4, in a basic solution, the values of the non-basic variables (a total of \(n - m\)) are zero. Therefore, among \(\lambda_1, \dots, \lambda_n\), at most \(m\) can be non-zero.
(b) Let \(y\) be a point in \(P\). Transform \(P\) into standard form:
Since it is a non-empty standard form polyhedron, there exists a basic feasible solution. According to Theorem 2.4, the values of the non-basic variables (a total of \( n - m - 1 \)) are zero. Therefore, among \( \lambda_1, \dots, \lambda_n \), at most \( m + 1 \) can be non-zero.
Comment: This problem mainly examines the property that a non-empty standard form polyhedron must have a basic feasible solution (the form of a standard form polyhedron is \( \{ \mathbf{Ax = b, x \geq 0} \} \)).
Note
The geometric significance of Carathéodory’s theorem is that any point in an \( m \)-dimensional convex hull can be represented by a convex combination of at most \( m + 1 \) points from the convex hull.
Exercise 2.7#
Suppose that \(\{\mathbf{x}\in \mathcal{R}^n\mid \mathbf{a'_ix\geq b_i, i=1,\dots,m}\}\) and \(\{\mathbf{x}\in \mathcal{R}^n\mid \mathbf{g'_ix\geq h_i, i=1,\dots,k}\}\) are two representations of the same nonempty polyhedron. Suppose that the vectors \(\mathbf{a_1,\dots, a_m}\) span \(\mathcal{R}^n\). Show that the same must be true for the vectors \(\mathbf{g_1,\dots, g_k}\).
Solution:
Let the polyhedron be \(P\). Suppose that \(\mathbf{g}_1, \dots, \mathbf{g}_k\) cannot generate \(\mathcal{R}^n\). Then there exists a vector \(\mathbf{d}\) in \(\mathcal{R}^n\) that is orthogonal to all of \(\mathbf{g}_1, \dots, \mathbf{g}_k\). For any point \(\mathbf{x}_0\) that satisfies \(\{\mathbf{x} \in \mathcal{R}^n \mid \mathbf{g}_i' \mathbf{x} \geq h_i, i = 1, \dots, k\}\), \(\mathbf{x}_0 + \mathbf{d}\) is also inside \(P\), meaning that \(P\) contains a line. However, since \(\mathbf{a}_1, \dots, \mathbf{a}_m\) can generate \(\mathcal{R}^n\), there are \(n\) linearly independent vectors among \(\mathbf{a}_1, \dots, \mathbf{a}_m\). According to Theorem 2.6, \(P\) cannot contain a line, which is a contradiction. Therefore, \(\mathbf{g}_1, \dots, \mathbf{g}_k\) must also generate \(\mathcal{R}^n\).
Exercise 2.8#
Consider the standard form polyhedron \(\{\mathbf{x} \mid \mathbf{Ax = b}, \mathbf{x} \geq 0\}\), and assume that the rows of the matrix \(\mathbf{A}\) are linearly independent. Let \(\mathbf{x}\) be a basic solution, and let \(J = \{i \mid x_i \neq 0\}\). Show that a basis is associated with the basic solution \(\mathbf{x}\) if and only if every column \(\mathbf{A}_i, i \in J\), is in the basis.
Solution:
Proof. (1) First, we prove that if each column vector \(\mathbf{A}_i, i \in \mathbf{J}\) is in the basis, then these column vectors correspond to a basic solution \(\mathbf{x}\).
Let \(\mathbf{B}=[\mathbf{A_{B(1)}, \dots, A_{B(m)}}]\) be the basis. Since each column vector \(\mathbf{A}_i, i \in \mathbf{J}\) is in the basis \(\mathbf{B}\), they are linearly independent. Also since \(\mathbf{A}\) is full row ranked, any \(m\) columns of \(\mathbf{A}\) is independent (fullfill Theorem 2.4 a). According to the problem statement, if \(j \notin \mathbf{J}\), then \(x_j = 0\) (fullfill Theorem 2.4 b). According to Theorem 2.4 in the textbook, \(\mathbf{x}\) is a basic solution.
(2) Next, we prove that if the column vectors \(\mathbf{A}_i, i \in \mathbf{J}\) correspond to a basic solution \(\mathbf{x}\), then they are in the basis.
According to Theorem 2.4, if \(i\neq \mathbf{B}(1),\dots, \mathbf{B}_m\), \(x_i=0\). According to the definition of \(\mathbf{J}\), \(\mathbf{J}\subset \{\mathbf{B}(1),\dots, \mathbf{B}_m\}\), so column vectors \(\mathbf{A}_i, i \in \mathbf{J}\) is in the basis.
\(\Box\)
Exercise 2.9#
Consider the standard form polyhedron \(\{\mathbf {x \mid Ax = b, x \geq 0}\}\), and assume that the rows of the matrix \(\mathbf{A}\) are linearly independent.
(a) Suppose that two different bases lead to the same basic solution. Show that the basic solution is degenerate.
(b) Consider a degenerate basic solution. Is it true that it corresponds to two or more distinct bases? Prove or give a counterexample.
(c) Suppose that a basic solution is degenerate. Is it true that there exists an adjacent basic solution which is degenerate? Prove or give a counterexample.
Solution:
(a) Consider a matrix \(\mathbf{A}\) with \(m\) rows and \(n\) columns, and two bases \(\mathbf{B}_1\) and \(\mathbf{B}_2\). Assume that both basic solutions are non-degenerate, meaning that all \(m\) variables in the basic solution corresponding to basis \(\mathbf{B}_1\) are non-zero, and all \(m\) variables in the basic solution corresponding to basis \(\mathbf{B}_2\) are also non-zero. Since the two bases are different, there is at least one variable that is in \(\mathbf{B}_1\) but not in \(\mathbf{B}_2\), which leads to \(m+1\) non-zero variables in the solution \(\mathbf{x}\). This contradicts the fact that \(\mathbf{x}\) is a basic solution. Therefore, the basic solution \(\mathbf{x}\) must be degenerate.
(b) No. The simple counter example is \(\{x=0, x\geq 0\}\). The degenerate basic solution is \(x=0\), but it corresponds to only one base.
(c) No. An counter example:
Base \(\{\mathbf A_1,\mathbf A_2\}\) and\(\{\mathbf A_2,\mathbf A_3\}\) all corresponds to a degenerate solution \([0, 1, 0]\). But the solution \([1, 0, 1]\) of their adjacent bas \(\{\mathbf A_1,\mathbf A_3\}\) is not degenerate.
Exercise 2.10#
Consider the standard form polyhedron \(P = \{\bf x \mid Ax = b, x \geq 0\}\). Suppose that the matrix \(\bf A\) has dimensions \(m \times n\) and that its rows are linearly independent. For each one of the following statements, state whether it is true or false. If true, provide a proof, else, provide a counterexample.
(a) If \(n = m + 1\), then \(P\) has at most two basic feasible solutions.
(b) The set of all optimal solutions is bounded.
(e) At every optimal solution, no more than \(m\) variables can be positive.
(d) If there is more than one optimal solution, then there are uncountably many optimal solutions.
(e) If there are several optimal solutions, then there exist at least two basic feasible solutions that are optimal.
(f) Consider the problem of minimizing \(\max\{\bf c'x, d'x\}\) over the set \(P\). If this problem has an optimal solution, it must have an optimal solution which is an extreme point of \(P\).
Solution:
(a) Right. The key is to prove that \(P\) is one-dimensional。
Proof.
Since the rows in \(\bf A\) are linear independent, rank(\(\bf A\)) \(=m\). Accodering to the knowledge in linear algebra,
Therefore, the dimensiion of the null space of \(\bf A\) is 1, i.e., the solution space of equations \(\bf Ax=0\) is 1. Accordering to linear algebra, the dimension of the solutio space is \(\bf Ax=b\) is equal to that in \(\bf Ax=0\) (becaause the general solution of \(\bf Ax=b\) equals to any feasible solution plus the solution of 的 \(\bf Ax=0\)).
Since the solution of \(P\) is the subset of the solutions in \(\bf Ax=b\), \(P\) is the subset of a line, i.e., \(P\) is a line segemen, point or empty space, all of which has at most two vertices. So, there are at most 2 basice feasible solutions for \(P\).
\(\Box\)
(b) Wrong. A counter example:
When \(x_2=0\) and \(x_1\) be any real number, it can be an optimal solution. So the set of optimal solutions is not bounded.
(c) Wrong. If the coefficients \(\bf c\) in the objective function are \(\bf 0\), any feasible solution are optimal and there can be more than \(m\) variables that are positive.
(d) Right. It is easy to verify the points on the line segment of two optimal soulutions are also optimal.
(e) Wrong. A counter example:
(0, 1) and (0, 2) are both optimal solutions, but there is only one basic feasible solution (0, 0).
(f) wrong. A counter example:
The objective of the above problem equals \(|x_1-1|\). The unique optimal solution is (1, 1), which is not an extreme point.
Note
For this nonlinear objetive function in a polyhron, the optimal solution may not be the extrem point.
The solution of \(n\) linear independent active constraints is basic solution (\(n\) is the number of variables).
Exercise 2.11#
Let \(P =\{x \in \mathcal{R}^n \mid \mathbf{Ax\geq b}\}\). Suppose that at a particular basic feasible solution, there are \(k\) active constraints, with \(k > n\). Is it true that there exist exactly \(k\choose n\) bases that lead to this basic feasible solution? Here \({k\choose k} = k! / (n! (k - n) !)\) is the number of ways that we can choose \(n\) out of \(k\) given items.
Solution:
No.There may be dependent constrains in the \(k\) active constraints. We can find a counter example:
In this example, \(k=2\), \(n=1\). However, there is only 1 base that leads to the basic feasible solution.
Exercise 2.12#
Consider a nonempty polyhedron \(P\) and suppose that for each variable \(x_i\) we have either the constraint \(x_i\geq 0\) or the constraint \(x_i\leq 0\). Is it true that \(P\) has at least one basic feasible solution?
Solution:
Yes. For all the constraints \(x_i\geq 0\) or the constraint \(x_i\leq 0\), there are \(n\) of them that are independent. According to Theorem 2.6 (c), there exists a basic feasible solution for this nonempty polyhedron.
Note
According to Theorem 2.6, there must exist a basic fesible solution in a non-empty polyhedron if there are \(m\) linear independent row coefficients constraints.
Exercise 2.13#
Consider the standard form polyhedron \(P = \{\mathbf x \mid\mathbf Ax = \mathbf b, x \geq 0\}\). Suppose that the matrix \(\mathbf{A}\), of dimensions \(m \times n\), has linearly independent rows, and that all basic feasible solutions are nondegenerate. Let x be an element of \(P\) that has exactly \(m\) positive components.
(a) Show that x is a basic feasible solution.
(b) Show that the result of part (a) is false if the nondegeneracy assumption is removed.
Solution:
(a) Proof.
We apply Theorem 2.4 to prove it. Since \(\mathbf x\) has \(m\) positive components, let \(B(1), \dots, B(m)\) be its correponding indices. This already satifies Theorem 2.4 (b) that if \(i\neq B(1),\dots,B(m)\), \(x_i=0\). Now we need to prove Theorem 2.4 (a) that the columns \(\mathbf{A}_{B(1)},\dots,\mathbf{A}_{B(m)}\) are linear independent. We prove it by contradiction.
If the columns \(\mathbf{A}_{B(1)},\dots,\mathbf{A}_{B(m)}\) are linear dependent, there exists one columnn that can be the linear combination of others. We suppose this column be \(\mathbf{A}_{B(m)}\), i.e.,
Since
by putting (2) to (1), we have:
Since the matrix \(\mathbf{A}\) has \(m\) independent rows, it must also have \(m\) independent columns. We can find another column \(\mathbf{A}_{B(k)}\), \(k\neq B(1),\dots, B(m)\) that is independent with \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(m-1)}\). And because \(\mathbf{Ax=b}\),
if \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(m-1)}\) are independent, this will result in a basic feasible solution \(\left(x_{B(1)}+\alpha_1 x_{B(m)},\dots, x_{B(m-1)}+\alpha_{m-1}x_{B(m-1)}, 0\right)\), which is degenerate and contradicts with the fact all basic solutions are nondegenerate.
if \(\mathbf{A}_{B(1)},\dots, \mathbf{A}_{B(m-1)}\) are dependent, find the independent columns from them, and replenish with some remaining columns from the matrix \(\mathbf{A}\) to get \(m\) independent columns. Repeat a similar procedure as above from (1) to (3), this will also lead to a degenerate basic feasible solution, which contradicts the nondegerate fact.
\(\Box\)
(b) An counter example.
A standard polyhedron:
One solution (1,4,0) is not a basic feasible solution.
Exercise 2.14#
Let \(P\) be a bounded polyhedron in \(\mathcal{R}^n\) , let \(\mathbf a\) be a vector in \(\mathcal{R}^n\) ,and let \(b\) be some scalar. We define
Show that every extreme point of \(Q\) is either an extreme point of \(P\) or a convex combination of two adjacent extreme points of \(P\).

Solution:
Proof.
Assume the polyhedron \(P\) is \(\{\mathbf{x}\in \mathcal{R}^n\mid\mathbf{A_1x=b_1}, \mathbf{x}\geq 0\}\), then \(Q\) can be written as:
Assume \(\mathbf{x}^{\ast}\) is an extreme point of \(Q\). Since the extreme point is also a basic feasible solution (Theorem 2.3), from the definition of 2.9, there are \(n\) independent active constraints at \(\mathbf{x}^{\ast}\). Thre are two scenarios:
(1) if the \(n\) independent active constraints are all in \(\mathbf{A_1x=b_1}\), then \(\mathbf{x^{\ast}}\) is the basic feasible solution of \(P\) by definition 2.9 and also an extreme point of it.
(2) if \(\mathbf{a'x}=b\) is also an active constraint in them, then there are \(n-1\) independent active constraints in \(\mathbf{A_1x=b_1}\). Let \(I\) represent the row index in \(\mathbf{A_1x=b_1}\)that are active consraints, i.e., \(I=\{i\mid \mathbf{a'^i_1x}=b^i_1\}\). Then all the \(\mathbf{a'}_1^i (i\in I)\) lie in a proper subspace of \(\mathcal{R}^n\). There exists a non-zero vector \(\mathbf{d}\) that are orthogonal to every \(\mathbf{a'}_1^i (i\in I)\), i.e., \(\mathbf{a'}_1^i\mathbf{d}=0\). Let us consider a line:
where \(\lambda\) is an arbitrary scalar. For all \(i\in I\), \(\mathbf{a'}_i^1(\mathbf{x}^\ast+\lambda\mathbf{d})=0\), thus the active constraints remain active at all points on this line. If we vary the values of \(\lambda\), some of the original active constraints will eventually be violated. Bus since \(P\) is a bounded polyhedron,it does not contain a line. At the point where the orginal active constraints is about to be violated, there will be a new active constraint: \(\mathbf{a'_j}(\mathbf{x}^\ast+\lambda\mathbf{d})=b_j\). \(\mathbf{a'_2}\) is independent with \(\mathbf{a'}_1^i (i\in I)\) because if not so, it will be a linear combination of \(\mathbf{a'}_1^i (i\in I)\) and \(\mathbf{a'}_j\mathbf{x}^\ast=b_j\), which contradicts the definiton of \(I\) (\(j\) should also be in \(I\) but it not). Hence, \(\mathbf{a'}_j\mathbf{x}^\ast\neq b_j\) and \(\mathbf{a'_jd}\neq 0\). By moving from \(\mathbf{x^\ast}\) to \(\mathbf{x^\ast}+\lambda\mathbf{d}\), we now have \(n\) active constraints and the point is an extreme point of \(P\).
Since \(\lambda\) can be both positive and negative, we have two directions along the line \(y=\mathbf{x}^\ast+\lambda\mathbf{d}\) and will reach two extreme points of \(P\), which have \(n-1\) same indepedent active constraints and are adjacent. The point \(\mathbf{x^\ast}\) lies in the line segment between the two extreme points and it is a convex combination of them.
\(\Box\)
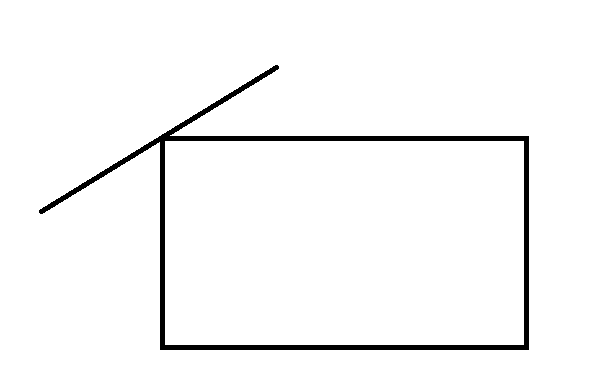
The above two figures shows the situation when \(P\) is a rectangular and \(Q\) is a line.
Exercise 2.15#
(Edges joining adjacent vertices) Consider the polyhedron \(P = \{\mathbf{x} \in \mathcal{R}^n \mid \mathbf{a'_ix} \geq b_i, i = 1,\dots, m\}\) . Suppose that \(\mathbf u\) and \(\mathbf v\) are distinct basic feasible solutions that satisfy \(\mathbf{a'_iu} = \mathbf{a'_iv} = b_i , i = 1, \dots, n - 1\), and that the vectors \(\mathbf{a}_l,\dots, \mathbf{a}_{n- 1}\) are linearly independent. (In particular, \(\mathbf u\) and \(\mathbf v\) are adjacent.) Let \(L = \{\lambda\mathbf{u} + (1 - \lambda)\mathbf{v}\mid 0\leq\lambda\leq 1\}\) be the segment that joins \(\mathbf u\) and \(\mathbf v\). Prove that \(L = \{\mathbf{z}\in P \mid \mathbf{a'}_iz = b_i , i = 1, \dots, n - 1\}\) .
Solution:
Proof.
In the polyhedron \(\{\mathbf{z}\in P \mid \mathbf{a'_iz} = b_i, i = 1,\dots, n-1\}\), there are \(n-1\) independent rows and \(n\) columns. From Exercise 2.10 (a), there are at most 2 basic feasible solutions. Since \(\mathbf{u}\) and \(\mathbf{v}\) are two of them, \(\mathbf{u}\) and \(\mathbf{v}\) are exactly the 2 extreme points in it and it is a line segment. And it is bounded for this line segment.. According to Theorem 2.9, a bounded polyhedron is the convex hull of its extreme points. \(L = \{\lambda\mathbf{u} + (1 - \lambda)\mathbf{v}\mid 0\leq\lambda\leq 1\}\) is just the convex hull of extreme points \(\mathbf{u}\) and \(\mathbf{v}\).So it equals to the polyhedron \(\{\mathbf{z}\in P \mid \mathbf{a'_iz} = b_i, i = 1,\dots, n-1\}\).
\(\Box\)
Exercise 2.16#
Consider the set \(\{\mathbf{x} \in \mathcal{R}^n \mid x_l = \dots = x_{n- l} = 0, 0\leq x_n\leq 1\}\) .Could this be the feasible set of a problem in standard form?.
Solution:
No, we prove it by contradiction. From the given feasible set, we can see that \(x_1=\dots=x_n=0\) is a feasible solution to the problem. For the polehedron in standard form \(\{\mathbf{Ax=b, x\geq 0}\}\), we get \(\mathbf{A0=0}\), i.e., \(\mathbf{b=0}\).
From the given feasible set, we can also see that \(x_1=\dots,=x_{n-1}=0,x_n=1\) is also a feasbile solution, i.e.,
But
Therefore, \(x_1=\dots=x_{n-1}=0,x_n={2}\) is also a feasible solution, which contradicts with the definiton of the given feasible set. So the set can not be the feasible set of problem in standard form.
\(\Box\)
Exercise 2.17#
Consider the polyhedron \(\{\mathbf{x} \in \mathcal{R}^n \mid \mathbf{Ax \leq b, x \geq 0}\}\) and a nondegenerate basic feasible solution \(\mathbf{x}^*\) . We introduce slack variables \(\mathbf{z}\) and construct a corresponding polyhedron \(\{\mathbf{(x, z)\mid Ax + z = b, x \geq 0, z \geq 0}\}\) in standard form. Show that \((\mathbf{x^* , b-Ax^*})\) is a nondegenerate basic feasible solution for the new polyhedron.
Solution:
Proof.
Assume there are \(m\) rows in \(\mathbf{A}\). We represent the original polyhedron as \(P_0\) and the new polyhedron as \(P_1\).
(1) Apprently, \((\mathbf{x^* , b-Ax^*})\) is feasible for \(P_1\).
(2) Next, we show that it is a baisc solution for \(P_1\). To do so, we must show there are \(m+n\) independent constraints that are active in \((\mathbf{x^* , b-Ax^*})\).
Since \(\mathbf{x}^\ast\) is a nondegenerate basic feasible solution, there are \(n\) independent active constraints in the polyhedron \(\{\mathbf{x} \in \mathcal{R}^n \mid \mathbf{Ax \leq b, x \geq 0}\}\). Without loss of generality, we assume there are \(k\) constraints in \(\mathbf{Ax\leq b}\) and \(l\) constraints in \(\mathbf{x}\geq 0\) that are independent active (\(k+l=n, k\leq m\)).
Those original \(n\) constraints in \(P_0 \) are also independent active in \(P_1\). For the \(k\) active constraints in \(\mathbf{Ax\leq b}\) of \(P_0\), in \(P_1\) they becomes \(\mathbf{Ax+0=b}\), i.e., there are \(k\) components of \(\mathbf{z}\) that are 0. That is, there are \(k\) independent active constraints in \(\mathbf{z}\geq 0\) of \(P_1\). Now we already have \(k+n\) independent active constarints in \(P_1\).
For the remnant \(m-k\) constraints in \(\mathbf{Ax\leq b}\) of \(P_0\), they may be non active or dependent with the \(k\) active constraints.
For those that are non active in \(P_0\), i.e., \(\mathbf{Ax<b}\), the corresponding constraints \(\mathbf{Ax+z=b}\) in \(P_1\) are independent active.
For those that are dependent on the \(k\) active constraints, their corresponding constraints in \(P_1\) results in \(\mathbf{z}=0\), which are also independent active.
For either of the two above situation, it results in \(m-k\) independet active constraints. In total, we have \(m-k+k+n=m+n\) independent active constraints in \((\mathbf{x^* , b-Ax^*})\). Now, we have proved it is a basic feasible solution for \(P_1\).
(3) Last, we show that it is nondegenerate. We do it by using contradiction.
If \((\mathbf{x^* , b-Ax^*})\) is a degenerate basic feasible solution for \(P_1\), there are more than \(m+n\) independent active constraints.
By the proof of (2), there are \(m+n\) independent active constraints in \(\mathbf{Ax\leq b}\), \(\mathbf{z\geq 0}\) and part of \(\mathbf{x}\geq 0\). So if we want to have more than \(m+n\) independent active constraints, we must find it in \(\mathbf{x}\geq 0\). But this will result more than \(n\) indepedent active constraints in \(P_0\), which contradicts with the argument that \(\mathbf{x}^\ast\) is a nondegenerate basic feasible solution of \(P_0\).
Exercise 2.18#
Consider a polyhedron \(P = \{\mathbf{x \mid Ax \leq b}\}\). Given any \(\epsilon > 0\),show that there exists some \(\overline{\mathbf{b}}\) with the following two properties:
(a) The absolute value of every component of \(\mathbf{b - \overline{b}}\) is bounded by \(\epsilon\).
(b) Every basic feasible solution in the polyhedron \(P = \{\mathbf{x \mid Ax \leq \overline{b}}\}\) is nondegenerate
Solution:
Proof.
(a) for any element of \(\mathbf{b}\), since \(b_i\) is a real number, there exists a \(\epsilon\) neighborhood, i.e., for any \(\epsilon>0\), the \(\epsilon\) neighborhood of \(b_i\) is:
Hence, we can find \(\overline{b}_i\) in the neighbourhood \(V_i\) for any elements in \(\mathbf{b}\) to satisfy the requirement.
(b) for any feasible solution \(\mathbf{x}^\ast\), if this solution is degenerate in \(P\), it means that there are excessive active constraints at \(\mathbf{x}^\ast\). For any excessive active constraint \(\mathbf{a'x^\ast}\leq b_i\), we an change the value of \(b_i\) a little bit by select one value from its \(\epsilon\) neighborhood to make this constraint nonactive at \(\mathbf{x}^\ast\). Repeat this procedure, we can make all the excessive constraint unactive at \(\mathbf{x}^\ast\). Hence, we can find the values of \(\mathbf{\overline{b}}\) to make every basic feasible solution in the polyhedron nondegenerate.
\(\Box\)
Exercise 2.19*#
Let \(P\in R^n\) be a polyhedron in standard form whose definition involves \(m\) linearly independent equality constraints. Its dimension is defined as the smallest integer \(k\) such that \(P\) is contained in some k-dimensional affine subspace of \(\mathcal{R}^n\).
(a) Explain why the dimension of \(P\) is at most \(n - m\).
(b) Suppose that \(P\) has a nondegenerate basic feasible solution. Show that the dimension of \(P\) is equal to \(n - m\).
(c) Suppose that \(\mathbf x\) is a degenerate basic feasible solution. Show that \(\mathbf x\) is degenerate under every standard form representation of the same polyhedron (in the same space \(\mathcal{R}^n\)) . Hint: Using parts (a) and (b) , compare the number of equality constraints in two representations of \(P\) under which \(\mathbf x\) is degenerate and nondegenerate, respectively. Then, count active constraints.
Solution:
(a)
If there is no feasible solutions in \(P\), i.e., \(P\) is empty, then the dimension of \(P\) is 0.
If there exists a feasible soltion, without loss of generality, we assume \(P=\{\mathbf{x\mid Ax=b}\}\) and the feasible solution is \(\mathbf{x}_0\).
Hence, \(\mathbf{Ax_0=b}\) and \(\mathbf{A(x-x_0)=0}\). The dimension of \(P\) is the dimension of the null space of \(\mathbf{A}\) in the set of equations \(\mathbf{A(x-x_0)=0}\).
By the Rank Theoreom,
Since \(P\) involves \(m\) linear independent equality constraints, \(\text{rank}(\mathbf{A})\geq m\) (or else there is no feasible solution for \(P\) and its dimension is 0), \(\text{dim}(\text{Nul}(A))\leq n-m\).
Therefore, bases on the two above situations, the dimension of \(P\) is at most \(n-m\).
(b) If \(P\) has a nondegerate basic feasible solution, there are exactly \(m\) linear independent active constraints at this feasible solution and \(\text{rank}(A)=m\). By the equation (1), the dimension of \(P\) is equal to \(n-m\).
(c) For two standard form representations of \(P\), \(\mathbf{x}\) is a degenerate basic feasible solution for representation one. Hence, there are more than \(m\) independent active constraints at \(\mathbf{x}\) and the dimension of \(P\) is at larger than \(n-m\). If \(\mathbf{x}\) is nondegerate for representation two, there is a contradiction that the dimension of \(P\) is equal to \(n-m\) by the conclusion of (b).
Therefore, \(\mathbf{x}\) is degenerate under every stand form representation.
Exercise 2.20 *#
Consider the Fourier-Motzkin elimination algorithm.
(a) Suppose that the number \(m\) of constraints defining a polyhedron \(P\) is even. Show, by means of an example, that the elimination algorithm may produce a description of the polyhedron \(\Pi_{n-1}(P)\) involving as many as \(m^2/4\) linear constraints, but no more than that.
(b) Show that the elimination algorithm produces a description of the one-dimensional polyhedron \(\Pi_1(P)\) involving no more than \(m^{2^{n-1}}/2^{2^n-2}\) constraints.
(c) Let \(n = 2^P +p+ 2\), where \(p\) is a nonnegative integer. Consider a polyhedron in \(\mathcal{R}^n\) defined by the \(8 {n \choose 3}\) constraints
where all possible combinations are present. Show that after \(p\) eliminations, we have at least
constraints. (Note that this number increases exponentially with \(n\).)
Solution:
Proof.
(a) If the number of constraints is even, in the elimination algorithm to produce the polyhedron \(\Pi_{n-1}(P)\), the biggest number of invovled linear constraints happens when there are \(m/2\) constraints that the coefficient \(a_{i,n}\) for \(x_n\) is positive, while the other \(m/2\) constraints that \(a_{i,n}\) is negative (\(i=1,\dots,m\)). (If there are \(k\) constraints that \(a_{i,n}\) are positive and \(m-k\) other constraints that \(a_{i,n}\) are negative, then the total number of involved constraints is \(k(m-k)\). By GM-AM inequality, \(k(m-k)\leq (\frac{k+m-k}{2})^2=\frac{m^2}{4}\))
Hence, there are at most \(\frac{m}{2}\times\frac{m}{2}=\frac{m^2}{4}\) involved constraints.
(b) we prove it by intruduction.
Base case: When \(n=2\), it is trivial that the production of the one-dimensional polyhedron invoving no more than
\(m^{2^{n-1}}/2^{2^n-2}=m^2/4\) constraints.
Induction step: Assume that when \(n=k\), the production of one-dimensional polyhedron invovles no more than \(m^{2^{k-1}}/2^{2^k-2}\) constraints with \(m\) constraints in the \(k\) dimensional polyhedron. We now prove that the statement holds for \(n=k+1\).
When \(n=k+1\), if the number of the constraints \(m\) is even, the elimination from \(k+1\) dimension to \(k\)-dimensional polyhedron involves \(m^2/4\) constraints. By the assumption, the number of involved constraints to eliminate the dimension from \(k\) to \(1\) involves:
constraints, which meets the requirement; if \(m\) is old, the number of invovled constraints is no more than the situation when there are \(m-1\) constraints, which also meets the requirement. Now the proof is complete.
(c) After \(p\) eliminations, we eliminate the dimension of the polyhedron \(P\) from \(2^p+p+2\) to \(2^p+2\) and there are still \(2^p+2\) variables left in the polyhedron. We first show that since \(n=2^p+p+2\), if we eliminate one variable with minimum index in the remnant variables one time (i.e., eliminate \(x_1\) in the first elimination, eliminate \(x_2\) in the second elimination, and so on), after \(p\) elimnations, we have at least some constraints of the following form:
Base case: If \(p=1\), \(n=5\). There are constraints \(\pm x_1\pm x_2 \pm x_3\leq 1\), \(\pm x_1\pm x_4 \pm x_5\leq 1\) (they only share one varible \(x_1\)) in the polyhedron. After eliminating \(x_1\) from the two sets of constraints, we can get:
i.e, the base case hold.
Induction step: Assume after \(k\) eliminations, we have at least the following constraints (we replace \(n\) with \(2^k+k+2\) in the formula (1)):
Now we prove the situation after \(k+1\) eliminations. When \(p=k+1\), there are \(n=2^{k+1}+k+3\) variables.
Since we can find another set of constraints below after the \(k_{\text{th}}\) elimination (when we eliminate \(k\) times from the constraints with 3 variables in the set \(x_1\), \(x_2\), \(\dots\), \(x_{k+1}\), \(x_{2^k+k+3}\), \(\dots\), \(x_{2^{k+1}+k+3}\) from the original polyhedron. Recall that there are \(2^k+k+2\) variables in the above set),
which only share one variable with formula (2). By eliminating \(x_{k+1}\) from (2) and (3), we can get the following constraints:
which meets the requirement.
Since formula (1) holds after \(p\) eliminations, there are actually \(2^{2^p+2}\) constraints in the formula (1).
\(\Box\)
Note
the proof for (c) is non-trivial!
Exercise 2.21#
Suppose that Fourier-Motzkin elimination is used in the manner described at the end of Section 2.8 to find the optimal cost in a linear programming problem. Show how this approach can be augmented to obtain an optimal solution as well.
Solution:
At page 74 in the text book, we know that by adding a new variabel \(x_0\) and making it euqal to the objective function, i.e., \(x_0=c'x\), we can get the optimal cost after eliminating the polyhedron \(n\) times with only variable \(x_0\) in it.
Let us find the solution by backtracking. We use the same notations as at Page 72 in the text book. After eliminating \(n\) times, there are only one variable \(x_0\) in the constraints in the following form:
From the process of eliminating \(x_1\) in the previous elimnation, we know that:
and
With the above two sets of constraints in which there is only one unknow variable \(x_1\) in them, we can get a value of \(x_1\) since two constraints among them will force one exact value for \(x_1\) (it is because that the smallest element of \(x_0\) happens at one constraint in (1) that the left hand side is equal to the right hand side, while that means the left hand side of one constraint from (2) is equal to the left hand side of another constraint from (3). This will force one value for \(x_1\))
Repeat this process, we can get all other values of the solution.
Exercise 2.22#
Let \(P\) and \(Q\) be polyhedra in \(\mathcal{R}^n\). Let \(P + Q = \{\mathbf{x + y} \mid x \in P, \mathbf{y} \in Q\}\).
(a) Show that \(P + Q\) is a polyhedron.
(b) Show that every extreme point of \(P + Q\) is the sum of an extreme point of \(P\) and an extreme point of \(Q\).
Solution:
Proof.
(a) Let \(P=\{\mathbf{x\mid A_1x\geq b_1}\}\) and \(Q=\{\mathbf{y\mid A_2y\geq b_2}\}\). We can make another polyhedron \(M\) as follows
Then we can use Fourier-Motzkin method to eliminate the variables \(\mathbf{x, y}\) and only keep \(\mathbf{z}\). After the elimination, we get \(P+Q\). In other words, \(P+Q\) is the projection of \(M\) to the \(\mathbf{z}\) coordinates.
(b) We prove it by contradiction. If the extreme point \(z_0\) of \(P+Q\) is the sum of one non-extreme point \(x_0\) of \(P\) and another point \(y_0\) of \(Q\), then we can find two other points \(\mathbf{v_1, v_2}\) in \(P\) that \(\mathbf{x_0}=\lambda \mathbf{v_1}+(1-\lambda)\mathbf{v_2}\), in which \(0\leq \lambda\leq 1\). Hence,
Since \(\mathbf{v_1+y_0}\) and \(\mathbf{v_2+y_0}\) are also in \(P+Q\), it contradicts with the fact that \(\mathbf{z_0}\) is the extreme point of \(P+Q\). Another point is the extreme point of \(Q\) follows similarly.
\(\Box\)
Exercise 2.30#
If \(f\) is K-convex, \(\xi^x\) follows a Binomial distribution \(B(x, p)\) and \(|\mathbb{E}[f(x-\xi^x)]|<\infty\), then \(g(x)=\mathbb{E}[f(x-\xi^x)]\) is also K-convex.
Proof.
We prove it by the induction to the domain of \(g(x)\).
We first prove that \(g(x)\) is K-convex , we first show that:
i.e.,
Since
we can get:
The above formula holds because of the K-convexity of \(f(x)\). We then must also show that:
for any \(a\in\mathbb{Z^+}\).
Since
then
Let \(d(y) = \mathbb{E}[g(y+1-\omega^y)]\).
According to the law of total expectation,
So,
We must show
Since \(g(1)=\overline{p}d(0)+pg(0)\) and \(g(2)=\overline{p}d(1)+pg(1)\),
We must show
We must show
Now assume \(g(x)\) is K-convex for the dormain 0, 1,\(\dots\), \(n-1\), we now prove it is also K-convex for \(x=n\).
